Finite Automata

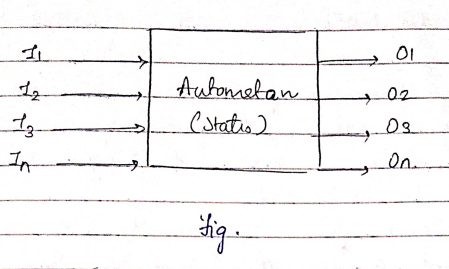
Finite automata is an abstract computing device. It is a mathematical model of a system with discrete inputs, outputs, states and a set of transitions from state to state that occurs on input symbols from the alphabet Σ.

The term finite is used because the number of possible states and the number of elements in the input Σ, both are finite. It is a good model for computer with limited amount of energy.

Finite automata is defined as a 5-tuples

M=(Q, Σ, δ,q0,F)

Where,

Q: Finite set called states.
Σ: Finite set called alphabets.
δ: Q × Σ → Q is the transition function.
q0 ∈ Q is the start or initial state.
F: Final or accept state.

mam diagram

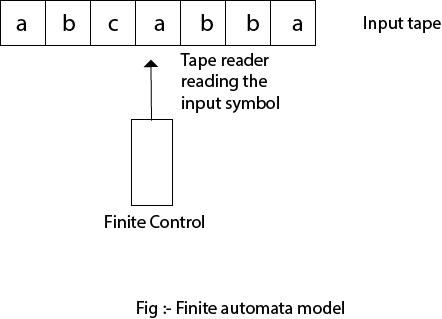
online diagram

Finite automata can be represented by input tape and finite control.

Input tape: It is a linear tape having some number of cells. Each input symbol is placed in each cell.

Finite control: The finite control decides the next state on receiving particular input from input tape. The tape reader reads the cells one by one from left to right, and at a time only one input symbol is read.

type of FA

Model of finite automata

mam diagram

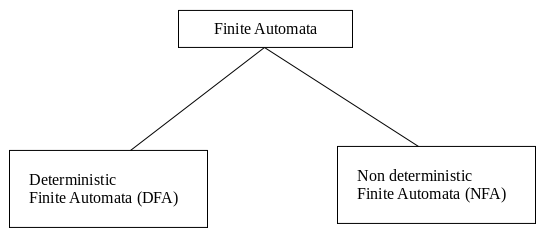
Deterministic Finite Automata

DFA refers to deterministic finite automata. Deterministic refers to the uniqueness of the computation. In the DFA, the machine goes to one state only for a particular input character. DFA does not accept the null move.

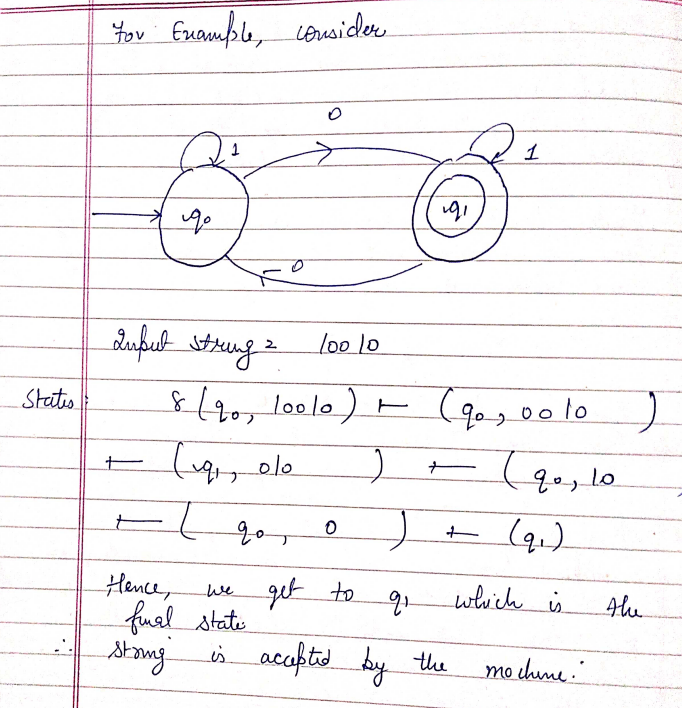
Acceptance by Finite Automata

mam diagram

Example for Acceptance of FA

mam diagram

Non-Deterministic Finite Automata

NFA stands for non-deterministic finite automata. It is used to transmit any number of states for a particular input. It can accept the null move.

Difference Between NFA and DFA?

Deterministic Finite Automata	Non-Deterministic Finite Automata
Each transition leads to exactly one state called as deterministic	A transition leads to a subset of states i.e. some transitions can be non-deterministic.
Accepts input if the last state is in Final	Accepts input if one of the last states is in Final.
Backtracking is allowed in DFA.	Backtracking is not always possible.
Requires more space.	Requires less space.
Empty string transitions are not seen in DFA.	Permits empty string transition.
For a given state, on a given input we reach a deterministic and unique state.	For a given state, on a given input we reach more than one state.
DFA is a subset of NFA.	Need to convert NFA to DFA in the design of a compiler.
δ : Q × Σ → Q For example − δ(q0,a)={q1}	δ : Q × Σ → 2 to the power Q For example − δ(q0,a)={q1,q2}
DFA is more difficult to construct.	NFA is easier to construct.
DFA is understood as one machine.	NFA is understood as multiple small machines computing at the same time.

Equivalence of DFA and NDFA

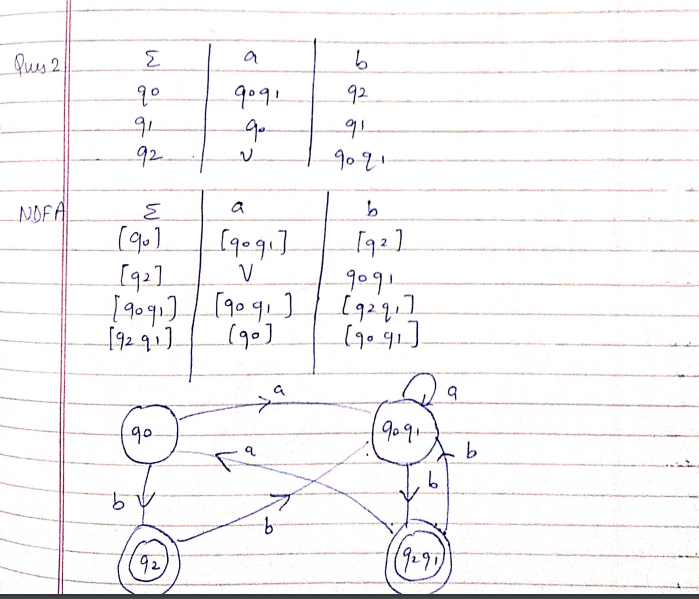
DFA to NDFA

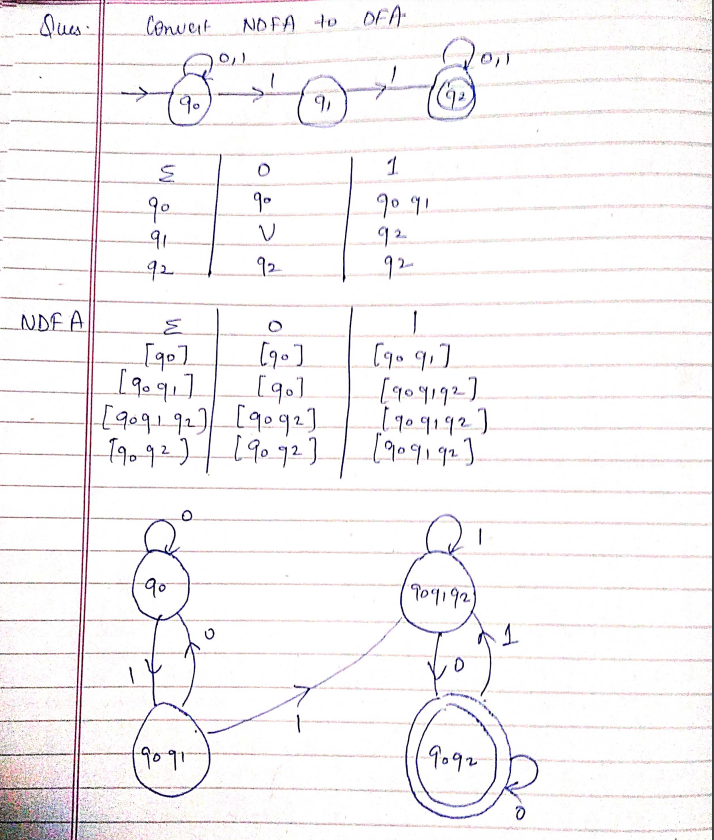
NDFA to DFA

Moore and Mealy machines

These are called finite auomata with output where as DFA and NDFA are known as finite automata without output.

Both moore and mealy machine are determinstic.

Mealy Machine

A Mealy Machine is an FSM whose output depends on the present state as well as the present input.

Output length should be n where is length of input string.

It can be described by a 6 tuple (Q, ∑, ▲, δ, λ, q0) where −

Q is a finite set of states.
∑ is a finite set of symbols called the input alphabet.
▲ is a finite set of symbols called the output alphabet.
δ is the input transition function where δ: Q × ∑ → Q
λ is the output transition function where λ: Q × ∑ → ▲
q0 is the initial state from where any input is processed (q0 ∈ Q).

Moore Machine

Moore machine is an FSM whose outputs depend on only the present state.

Output length should be n+1 where is length of input string.

A Moore machine can be described by a 6 tuple (Q, ∑, ▲, δ, λ, q0) where −

Q is a finite set of states.
∑ is a finite set of symbols called the input alphabet.
O is a finite set of symbols called the output alphabet.
δ is the input transition function where δ: Q × ∑ → Q
λ is the output transition function where λ: Q → ▲
q0 is the initial state from where any input is processed (q0 ∈ Q).

Equivalence of Moore and Mealy machine

Minimization of Finite Automata

The term minimization refers to the construction of finite automata with a minimum number of states, which is equivalent to the given finite automata. The number of states used in finite automata directly depend upon the size of the automata that we have used. So, it is important to reduce the number of states. We minimize the finite automata by detecting those states of automata whose presence or absence does not affect the language accepted by the finite automata.

Some important concepts used in the minimization of finite automata

Unreachable state
Dead State

Unreachable state: Unreachable state is that state in which finite automata never reaches during the transition from one state to another state.

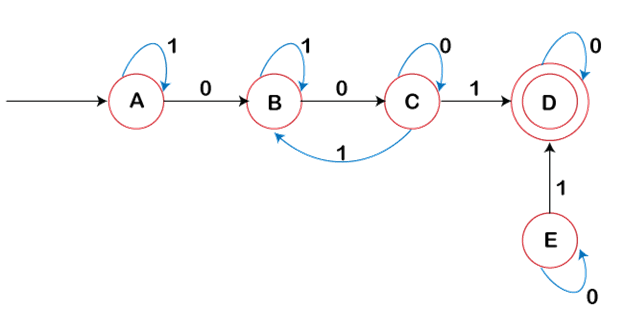
In the above DFA, we have unreachable state E, because on any input from the initial state, we are unable to reach to that state. This state is useless in finite automata. So, the best solution is to eliminate these types of states to minimize the finite automata.

Dead State: It is a non-accepting state, which goes itself for every possible input symbol.

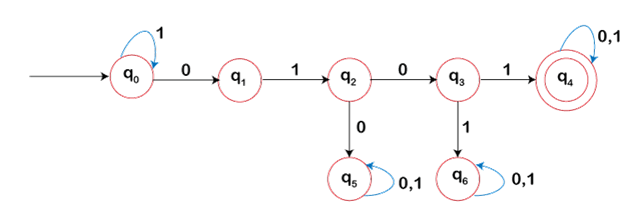
Dead State

In the above DFA, we have q5, and q6 are dead states because every possible input symbol goes to itself.

The following steps are used to minimize a Deterministic Finite Automata.

Step1: First of all, we detect the unreachable state.
Step2: After detecting the unreachable state, in the second step, we eliminate the unreachable state (if found).
Step3: Identify the equivalent states and merge them.
- In this, we divide all the states into two groups:
- Group A: This group contains all accepting states of automata.(final state)
- Group B: This group contains all non-accepting states of automata.(non final state)
This step is repeated for every group. Find group the input lead to if there are differences the partition the group into sets containing states which go to the same groups under the inputs.
The resulting final partition contains equivalent states now merge them into a single state.
Step4: In this step, we detect dead states.
Step5: After detecting the dead states, the last step is to eliminate dead states.

Applications and limitations of Finite Automata

Application

For the designing of lexical analysis of a compiler.
For recognizing the pattern using regular expressions.
For the designing of the combination and sequential circuits using Mealy and Moore Machines.
Used in text editors.
For the implementation of spell checkers.

Limitation