TOC-Short

TOC Formal Languages Finite Automata Regular Grammar Context Free Languages Pushdown Automata Context Sensitive Language Turing Machines

Formal Languages

Languages: The languages we consider for our discussion is an abstraction of natural languages. That is, our focus here is on formal languages that need precise and formal definitions. Programming languages belong to this category.

Symbols: Symbols are indivisible objects or entity that cannot be defined. That is, symbols are the atoms of the world of languages. A symbol is any single object such as a, 0, 1, #, begin, or do.

Basics of strings

A string or word over an alphabet Σ is a finite sequence of concatenated symbols of Σ .

Length of a string : The number of symbols in a string w is called its length, denoted by |w|.

Example : | 011 | = 4, |11| = 2, | b | = 1

Alphabets

Alphabets: An alphabet is a finite, nonempty set of symbols. The alphabet of a language is normally denoted by Σ.

Formal language

Chomsky Classification of languages

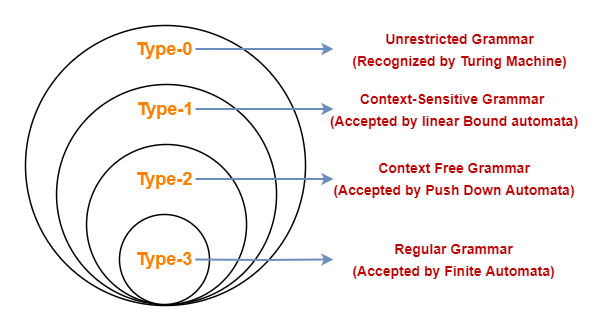
chomsky

Most famous classification of grammars and languages ​​introduced by Noam Chomsky is divided into four classes:

Noam Chomsky,is an American linguist,philosopher,cognitive scientist and social activist. Chomsky is well known in the academic and scientific community as one of the fathers of modern linguistics and a major figure of analitic philosophy.

Type₀ > Type₁ > Type₂ > Type₃

Variable is represented By Capital Alphabets where as Terminal are represented by small alphabets.

0 –Recursively enumerable grammar : Type-0 grammars (unrestricted grammars) include all formal grammars. They generate exactly all languages that can be recognized by a Turing machine. These languages are also known as the recursively enumerable languages. Note that this is different from the recursive languages which can be decided by an always-halting Turing machine.

Class 0 grammars are too general to describe the syntax of programming languages ​​and natural languages​​.

Expression

α -> β

α : (V + T)^+^
β : (V + T)^*^

V : Variable (Non-Terminal)
T : Terminal

1 –Context-sensitive grammars : Type-1 grammars generate the context-sensitive languages. These grammars have rules of the form α A β → α γ β with A a nonterminal and α,β and γ strings of terminals and nonterminals. The strings α and β may be empty,but γ must be nonempty. The languages described by these grammars are exactly all languages that can be recognized by a linear bounded automaton.

Expression

αAβ -> αγβ

A : non terminal or variable.
α, β and γ are string of terminal or non terminal.

String α, β can be empty but γ must be non-empty.

Example:

AB → CDB
AB → CdEB
ABcd → abCDBcd
B → b

2 –Context-free grammars : Type-2 grammars generate the context-free languages. These are defined by rules of the form A → γ with A a nonterminal and γ a string of terminals and nonterminals. These languages are exactly all languages that can be recognized by a non-deterministic pushdown automaton. Context-free languages are the theoretical basis for the syntax of most programming languages.

Expression

A -> α

A : single non terminal (Restriction)
α are string of terminal or non terminal or variable (V+T)*.

A is single non terminal

Example:

A → aBc

3 –Regular grammars : Type-3 grammars generate the regular languages. Such a grammar restricts its rules to a single nonterminal on the left-hand side and a right-hand side consisting of a single terminal,possibly followed (or preceded,but not both in the same grammar) by a single nonterminal. The rule S → ε is also allowed here if S does not appear on the right side of any rule. These languages are exactly all languages that can be decided by a finite state automaton. Additionally,this family of formal languages can be obtained by regular expresions. Regular languages are commonly used to define search patterns and the lexical structure of programming languages. Example:

A → ε
A →  a
A →  abc
A →  B
A →  abcB

interesting

If languages L1 and L2 are regular,are also regular the following languages:

L1 ∪ L2
L1 ∩ L2
L1 *  L2 ={xy:x ∈ L1 ∧ y ∈ L2}
L* ={ε} ∪ L ∪ L2 ∪ …

Operations on languages

Closure properties:

  1. Union
  2. Concatenation
  3. Complement
  4. kleen * closure
  5. Difference
  6. Intersection
  7. Reverse

1 2

Closure properties of language classes

Kleen Star (Σ*)

It is an infinite set of all possible strings over all posible length over alphabet (Σ), Excluding λ

Kleen Positive(Σ+)

It is an infinite set of all possible strings over all posible length over alphabet (Σ), including λ

Where λ is an null string.

TOC Formal Languages Finite Automata Regular Grammar Context Free Languages Pushdown Automata Context Sensitive Language Turing Machines
This site is open source. Improve this page.